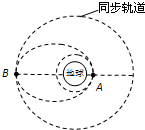
发射地球同步卫星时,可认为先将卫星发射至距地面高度为h1的圆形轨道上,在卫星经过A点时点火(喷气发动机工作)实施变轨进入椭圆轨道,椭圆轨道的近地点为A,远地点为B.在卫星沿椭圆轨道运动经过B点再次点火实施变轨,将卫星送入同步轨道(远地点B在同步轨道上),如图所示.两次点火过程都是使卫星沿切向方向加速,并且点火时间很短.已知同步卫星的运动周期为T,地球的半径为R,地球表面重力加速度为g,求:
(1)地球的第一宇宙速度
(2)卫星在圆形轨道运行接近A点时的加速度大小;
(3)卫星同步轨道距地面的高度.
(1)卫星作圆周运动向心力由重力提供即:
mg=mv2 R
解得:v=gR
(2)设地球质量为M,卫星质量为m,万有引力常量为G、卫星在近地圆轨道运动接近A点时的加速度为aA,在A点万有引力提供圆周运动向心力有:
G
=maA ①Mm (R+h1)2
又因为物体在地球表面上受到的万有引力等于重力
G
=mg ②Mm R2
由①和②解得:aA=
gR2 (R+h1)2
(3)设同步轨道距地面高度为h2,根据万有引力提供向心力有:、
G
=m(R+h2)Mm (R+h2)2
③4π2 T2
由②③两式解得:h2=
-R3 gR2T2 4π2
答:(1)地球的第一宇宙速度v=gR
(2)卫星在圆形轨道运行接近A点时的加速度大小为aA=
g;R2 (R+h1)2
(3)卫星同步轨道距地面的高度h2=
-R.3 gR2T2 4π2
