搜题请搜索小程序“爱下问搜题”
问题 填空题
椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的一个焦点为F1，若椭圆上存在一个点P，满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点，则椭圆的离心率为______．
答案

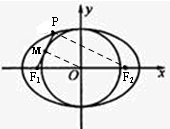
设以椭圆的短轴为直径的圆与线段PF1相切于点M，连结OM、PF2，

∵M、O分别为PF1、F1F2的中点，

∴MO∥PF2，且|PF2|=2|MO|=2b，

又∵线段PF1与圆O相切于点M，可得OM⊥PF1，

∴PF1⊥PF2，

∴|PF1|=

4c2-4b2
=2
c2-b2
．

∴|PF1|+|PF2|=2

c2-b2
+2b=2a，

化简得2ab=a2-c2+2b2=3b2，

∴b=

2
3
a，c=
5
3
a，

∴离心率为e=

c
a
=
5
3
．

故答案为：

5
3
．

单项选择题

安装了地面防喷器。用司钻法循环排盐水（不含气体）井涌。地面套压什么时候将达到最大值？（）

A.立即关井后。

B.在井涌循环到地面时。

C.在压井液进入立管时。

D.只有在井涌到达套管鞋时。

E.只是在压井液到达管柱后。
查看答案
问答题 简答题

国际环境合作原则的内容？
查看答案