问题
问答题
如图所示,质量为M="20" kg的平板车静止在光滑的水平面上;车上最左端停放着质量为m=5kg的电动车,电动车与平板车上的挡板相距L="5" m.电动车由静止开始向右做匀加速运动,经时间t=2s电动车与挡板相碰,问:
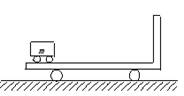
(1) 碰撞前瞬间两车的速度大小各为多少?
(2) 若碰撞过程中无机械能损失,且碰后电动机关闭并刹车,使电动车只能在平板车上滑动,要使电动车不脱离平板车,它们之间的动摩擦因数至少多大?
答案
(1)4m/s; 1m/s (2)µ≥0.2
(1)设两车从静止到碰撞前瞬间,平板车相对地发生的位移为x,则电动车相对地发生的位移为L-x.
由动量守恒定律,有:m-M=0
解得x="1" m
设碰前电动车、平板车的速度分别为V1、V2,因两车在碰前均做初速度为零的匀加速直线运动,由平均速度公式:V——==
V1=2×=…=4m/s
V2=2×=…=1m/s
(2) 因碰撞过程中系统动量守恒且无机械能损失,说明两车碰后分别以原速度大小沿相反方向运动
欲使电动车不脱离平板车,由能量守恒定律可知:
mV12+MV22≤µmgL
代入已知数据,可得:µ≥0.2
