问题
选择题
如图所示，质量均为m的小球A、B用长为L的细线相连，放在高为h的光滑水平桌面上（L＞2h），A球刚好在桌边。从静止释放两球，若A、B两球落地后均不再弹起，则下面说法中不正确的是
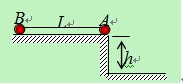
A、A球落地前的加速度为g/2
B、B球到达桌边的速度为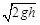
C、A、B两球落地的水平距离为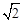
h
D、绳L对B球做的功为mgh/2
答案
答案：B
分析：对AB整体，受力分析可知，系统的机械能守恒，由于AB是通过同一条绳相连的，所以A落地之前它们的速度大小相等，B在平面上运动时，只有绳对B做功，由动能定理可以求得绳对B做功的大小．
解答：解：A、对AB整体受力分析，由牛顿第二定律可得，mg=2ma，所以a= g/2，所以A的说法正确．
B、对于AB组成的系统，机械能守恒，取地面为零势能面，则，2mgh=mgh+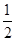
×2mV2，所以落地的速度也就是B球到达桌边的速度为V=
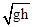，所以B的说法错误．
C、B球由于有了A球下落时的速度，所以B将做平抛运动，B的水平位移为x=Vt=×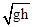
=
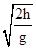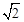h，所以C的说法正确．
D、绳只是在A落地之前对B有力的作用，对B受力分析知，只有绳对B做功，由动能定理可得W=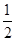mV2=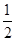mgh，所以D的说法正确．
由于本题选错误的，故选B．