滑块以初速度υ0=4m/s，从光滑斜面底端D向上做匀减速运动，先后

问题问答题

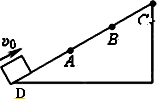
滑块以初速度υ₀=4m/s，从光滑斜面底端D向上做匀减速运动，先后通过A、B点，υ_A=2υ_B，到达斜面顶端C时，速度恰好减小为零，如图，已知A、B相距d=0.75m，滑块由B到C的时间t₀=0.5s，试求：

（1）滑块运动的加速度多大？

（1）斜面多长？

（2）滑块在斜面上滑到最高点的时间是多少？

答案

物块做匀减速直线运动，设A点的速度为v_A，B点的速度为v_B，加速度为a，斜面长为s

滑块运动时间为t₀

A到B：

=2asAB

v_A=2v_B

B到C：0=v_B+at₀

联立解得：v_B=1m/s，a=-2m/s²

D到C：0-

=2as

0=v₀+at

解得：s=4m．t=2s

答：（1）滑块运动的加速度是-2m/s²；

（1）斜面长4m；

（2）滑块在斜面上滑到最高点的时间是2s．