问题
问答题
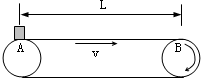
如图所示A、B分别为水平传送带的左右两端,绷紧的皮带以恒定的速度v=2m/s按如图所示方向传动,皮带和轮子不打滑.质量m=0.5kg的小物块无初速地放在A处.已知小物块与皮带间的动摩擦因数μ=0.1,g取10m/s2,小物块可视为质点.试分析下列情况:
(1)若小物块运动到B处时速度恰好为2m/s,则A、B间的距离L0=?
(2)若A、B间的距离L<L0,则小物块运动到B处的时间为多少?
(3)若A、B间的距离L>L0,则小物块运动到B处的时间是多少?
答案
(1)小物块的加速度a=μg=1m/s2
由vt2-
=2as可得L0=v 20
=v2 2a
=2m4 2×1
(2)若L<L0,则小物块从A运动到B一直做匀加速运动
由s=
at2可得所求时间:t=1 2
=2s a 2L
(3)若L>L0,则小物块先做匀加速运动至速度为2m/s,而后做匀速运动至B点.
匀加速运动的时间:t1=
=2s2L0 a
匀速运动的时间:t2=
=L-L0 v
-1L 2
可得所求时间:t=t1+t2=
+1L 2
答:(1)若小物块运动到B处时速度恰好为2m/s,则A、B间的距离为2m
(2)若A、B间的距离L<L0,则小物块运动到B处的时间为2L
(3)若A、B间的距离L>L0,则小物块运动到B处的时间是
+1L 2
