两根足够长的平行金属导轨，固定在同一水平面上，磁感应强度为B的匀强磁场与导轨所在平面垂直，方向竖直向下，导轨的电阻忽略不计，导轨间的距离为L，两根质量均为m的平行金属杆甲、乙可在导轨上无摩擦地滑动，滑动过程中与导轨保持垂直，每根金属杆接入回路的电阻都为R，在开始时刻，两杆都处于静止状态。现有一与导轨平行，大小为F的恒力作用于金属杆甲上，使金属杆在导轨上滑动。
(1)若某时刻甲的速度为v1，乙的速度为v2，求此时乙的加速度大小a乙；
(2)求由两金属杆与两金属导轨构成的回路中的最大感应电动势E。
(1)
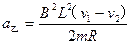(2)
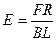
⑴由法拉第电磁感应定律，回路中的感应电动势大小为：
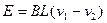① 4分
回路中的电流为：
② 1分
甲、乙两杆都受安培力作用，大小都为：
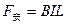③ 2分
乙杆受安培力方向水平向右，据牛顿第二定律有：
④ 2分
解以上各式得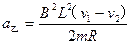： ⑤ 2分
⑵设乙的加速度为a乙时，甲的加速度为a甲，
甲杆受安培力方向水平向左，据牛顿第二定律有：
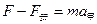⑥ 2分
开始时，a甲＞a乙，甲的速度增加得较快，所以甲、乙的速度之差
增大，由①式可知，E增大，由②③式可知I增大，F安增大，由④⑥式可知a甲减少，而a乙增大，当甲、乙两者加速度相等时，达最大值且稳定，此时回路电动势最大。 5分
由②③④⑥式和a甲＝a乙可得回路最大电动势为：
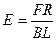⑦ 2分