问题
填空题
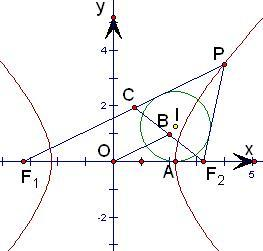
已知双曲线C:
①△PF1F2的内切圆的圆心在直线x=b上; ②△PF1F2的内切圆的圆心在直线x=a上; ③△PF1F2的内切圆的圆心在直线OP上; ④△PF1F2的内切圆必通过点(a,0); ⑤|OB|=e|OA|; ⑥|OB|=|OA|; ⑦|OA|=e|OB|; ⑧|OA|与|OB|关系不确定. 其中正确的命题的代号是______. |
答案
根据题意得F1(-c,0)、F2(c,0),
设△PF1F2的内切圆分别与PF1、PF2切于点A1、B1,与F1F2切于点A,
则|PA1|=|PB1|,|F1A1|=|F1A|,|F2B1|=|F2A|,
又点P在双曲线右支上,
所以|PF1|-|PF2|=2a,故|F1A|-|F2A|=2a,而|F1A|+|F2A|=2c,
设A点坐标为(x,0),
则由|F1A|-|F2A|=2a可得(x+c)-(c-x)=2a
解得x=a,则△PF1F2的内切圆必通过点(a,0),△PF1F2的内切圆的圆心在直线x=a上,
故②,④正确.
由于|OA|=a,在三角形PCF2中,由题意得,三角形PCF2是一个等腰三角形,PC=PF2,
∴在三角形F1CF2中,有:
OB=
CF1=1 2
(PF1-PC)=1 2
(PF1-PF2)=1 2
×2a=a.1 2
∴|OB|=|OA|.⑥正确.
故答案为:②,④,⑥.

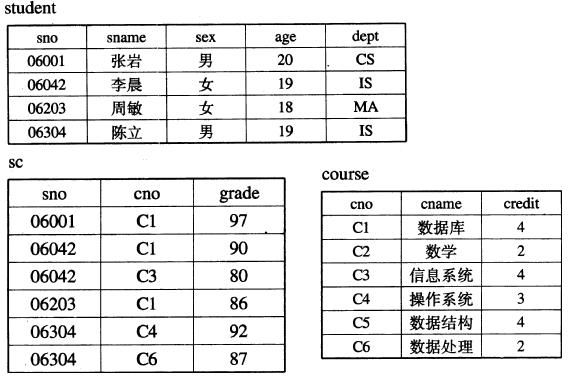 学生关系student的主码是sno,课程关系course的主码是cno,选课关系sc的主码是(sno,cno)。
学生关系student的主码是sno,课程关系course的主码是cno,选课关系sc的主码是(sno,cno)。