问题
填空题
已知点A(1,1)和点B(-1,-3)在曲线C:y=ax3+bx2+d(a,b,d为常数上,若曲线在点A和点B处的切线互相平行,则a3+b2+d=______.
答案
设f(x)═ax3+bx2+d,
∵f′(x)=3ax2+2bx,
∴f′(1)=3a+2b,f′(-1)=3a-2b.
根据题意得 3a+2b=3a-2b,∴b=0.
又点A(1,1)和点B(-1,-3)在曲线C上,
∴
解得:a+d=1 -a+d=-3 a=2 d=-1
a3+b2+d=7.
故答案为:7.

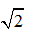
 W
W