问题
填空题
在三棱锥O-ABC中,M,N分别是OA,BC的中点,点G是MN的中点,则
|
答案
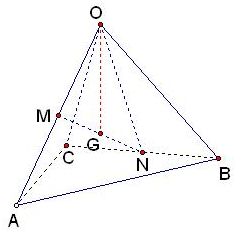
如图,连接ON,在△OBC中,点N是BC中点,则由平行四边形法则得
=ON
(1 2
+OB
)OC
在△OMN中,点G是MN中点,则由平行四边形法则得
=OG
(1 2
+OM
)ON
=1 2
+OM 1 2 ON
=1 4
+OA
•1 2
(1 2
+OB
)OC
(1 4
+OA
+OB
),OC
故答案为:
(1 4
+OA
+OB
).OC
