问题
计算题
宇航员站在某行星表面上一高处,沿水平方向抛出一个小球,经过时间t,小球落到行星表面,测得抛出点与落地点之间的距离为L,若抛出时的初速度增大为原来的2倍,抛出点与落地点之间的距离变为原来的1.5倍。已知两落地点在同一水平面内,该行星的半径为R,引力常量为G,求该行星的质量。
答案
解:设第一次抛出后小球水平位移为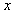 ,则第二次为2
,则第二次为2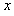
由几何关系可知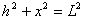 ①
①
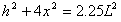 ②
②
由①②得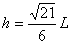
平抛运动竖直方向位移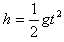 ③
③
根据牛顿第二定律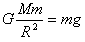 ④
④
由上式联立解得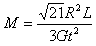

 中,填入A或V,并标出电流表和电压表的“+”“﹣”接线柱.
中,填入A或V,并标出电流表和电压表的“+”“﹣”接线柱.