（1）设P（x'，y'），得

PA

=（1-x'，1-y'），

PB

=（-1-x'，-1-y'），

所以

PA

•

PB

=（1-x'）（-1-x'）+（1-y'）（-1-y'）=（x'）²+（y'）²-2

∵

PA

•

PB

=2，

∴点P的轨迹方程为（x'）²+（y'）²-2=2，即（x'）²+（y'）²=4…（*）

再设D（x'，y'），由2

PD

=

PC

得D为PC的中点

∴x=

1

2

(x′+1)，y'=

1

2

y′．

可得x'=2x-1，y'=2y．代入（*）式得（2x-1）²+（2y）²=4

化简得点D的轨迹方程：（x-

1

2

）²+y²=1

（2）设点D坐标为（

1

2

+cosα，sinα），

求得直线AB的方程为x-y=0，得D到直线AB的距离为

d=

| 1 2 +cosα-sinα|

2

=

| 1 2 + 2 cos(α+ π 4 )|

2

当α=

7π

4

时，d的最大值为1+

2

2

，

因此△ABD面积的最大值为

1

2

×AB×（1+

2

2

）=1+

2

；

（3）若∠AMB为直角，则点M在以AB为直径的圆上

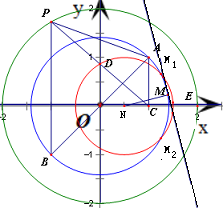
求得以AB为直径的圆方程为x²+y²=2，该圆与D的轨迹交于点M₁（

5

4

，

7

4

）和M₂（

5

4

，-

7

4

）

满足条件的点M位于圆N：（x-

1

2

）²+y²=1在x²+y²=2内的劣弧上

∵KNM1=

7 4 -0

5 4 - 1 2

=

7

3

，得此时切线l的斜率k₁=

1

KNM1

=-

3 7

7

KNM2=

- 7 4 -0

5 4 - 1 2

=-

7

3

，得此时切线l的斜率k₂=

1

KNM2

=

3 7

7

∴运动点M，观察斜率变化，可得直线l的斜率为k∈（-∞，-

3 7

7

）∪（

3 7

7

，+∞）