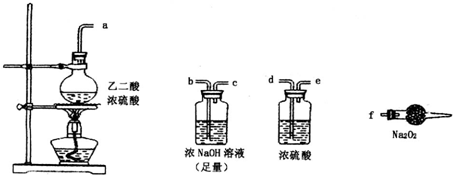
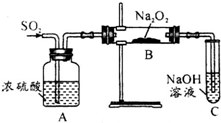
设F1、F2分别为椭圆C:
(1)若椭圆C上的点A(1,
(2)已知圆心在原点的圆具有性质:若M、N是圆上关于原点对称的两点,点P是圆上的任意一点,当直线PM、PN的斜率都存在,并记作KPM、KPN那么KPMKPN=-1.试对椭圆
|
(1)由题意知,2a=4,∴椭圆C的方程为
+x2 4
=1,把点A(1,y2 b2
)代入,得3 2
+1 4
=1,解得b2=3,c2=1,∴椭圆C的方程是9 4 b2
+x2 4
=1,焦点坐标是F1(-1,0),F2(1,0)y2 3
(2)在椭圆
+x2 a2
=1上取关于原点对称的两点M、N,在该曲线上任取不与M、N重合的动点P,直线PM,PN的斜率存在.那么kPM•kPN=-y2 b2 b2 a2
证明:设椭圆方程是
+x2 A
=1(A=a2,B=b2),设M(m,n),则N(-m,-n),又设P(x,y),(x≠±m,),那么y2 B
+m2 A
=1①且n2 B
+x2 A
=1②y2 B
因为kPM•kPN=(
)•(y-n x-m
)=y+n x+m
,由①知:n2=B-y2-n2 x2-m2
m2,由②y2=B-B A
x2,所以y2-n2=-B A
(x2-m2),所以kPM•kPN=B A
=-y2-n2 x2-m2
=-B A b2 a2