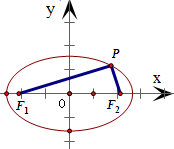
问题
选择题
设p为椭圆等
|
答案
∵m≥32,可得椭圆的焦点在x轴上
∴长轴2a=2
,c2=m+24m
∵△F1PF2中,cos∠F1PF2=5 13
∴|F1F2|2=|F1P|2+|PF2|2-2F1P•PF2cos∠F1PF2,
即4c2=(|F1P|+|PF2|)2-2F1P•PF2(1+cos∠F1PF2)
可得4c2=4a2-2F1P•PF2(1+
),得5 13
F1P•PF2=2a2-2c2=2b2=4818 13
∴F1P•PF2=104 3
∵sin∠F1PF2=
=1-(
)25 13 12 13
∴由正弦定理,得△PF1F2的面积为
S△PF1F2=
F1P•PF2sin∠F1PF2=1 2
×1 2
×104 3
=1612 13
故选:B