（1）90°（2）见解析

(1)解：以D为坐标原点，DA、DC、DD₁分别为x、y、z轴建立空间直角坐标系如图．

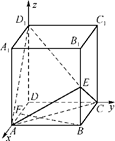
则相应点的坐标分别为D₁(0，0，2)，A(1，0，0)，C(0，1，0)，E(1，1，1)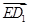，∴＝(0，0，2)－(1，1，1)＝(－1，－1，1)，

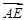＝(1，1，1)－(1，0，0)＝(0，1，1)，

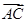＝(0，1，0)－(1，0，0)＝(－1，1，0)．

设平面AED₁、平面AEC的法向量分别为m＝(a，b，1)，n＝(c，d，1)．

由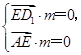

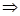
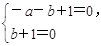
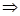
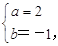
由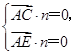

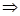
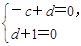
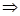
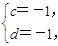
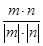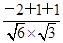∴m＝(2，－1，1)，n＝(－1，－1，1)，∴cosm，n=＝＝0，

∴二面角D₁AEC的大小为90°.

(2)证明：取DD₁的中点G，连结GB、GF.

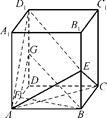
∵E、F分别是棱BB₁、AD的中点，

∴GF∥AD₁，BE∥D₁G且BE＝D₁G，

∴四边形BED₁G为平行四边形，∴D₁E∥BG.

又D₁E、D₁A平面AD₁E，BG、GF∥平面AD₁E，

∴BG∥平面AD₁E，GF∥平面AD₁E.

∵GF、GB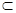平面BGF，∴平面BGF∥平面AD₁E.

∵BF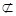平面AD₁E，∴直线BF∥平面AD₁E.

(或者：建立空间直角坐标系，用空间向量来证明直线BF∥平面AD₁E，亦可)