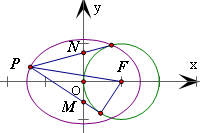
（I）设椭圆C的方程为

x2

a2

+

y2

b2

=1（a＞b＞0）

∵椭圆C的右焦点F是圆（x-1）²+y²=1的圆心F（1，0），

∴c=1，结合离心率e=

c

a

=

2

3

，得a=

3

2

因此，b²=a²-c²=

5

4

，得椭圆C的方程为

x2

9 4

+

y2

5 4

=1；

（II）设P（x₀，y₀），M（0，m），N（0，n），

可得直线PM的方程：y-m=

y0-m

x0

x，

化简得（y₀-m）x-x₀y+x₀m=0．

又圆心（1，0）到直线PM的距离为1，

∴

|y0-m+x0m|

(y0-m)2+x02

=1，

平方化简得（y₀-m）²+x₀²=（y₀-m）²+2x₀m（y₀-m）+x₀²m²，

整理可得（x₀-2）m²+2y₀m-x₀=0，同理可得（x₀-2）n²+2y₀n-x₀=0．

因此，m、n是方程（x₀-2）t²+2y₀t-x₀=0的两个不相等的实数根

∴m+n=

-2y0

x0-2

，mn=

-x0

x0-2

，

∴|MN|=|m-n|=

(m+n)2-4mn

=

4x02+4y02-8x0 (x0-2)2

．

∵P（x₀，y₀）是椭圆

x2

9 4

+

y2

5 4

=1上的点，

∴

x02

9 4

+

y02

5 4

=1，可得y02=

5

4

(1-

x02

9 4

)=

5

4

-

5

9

x02

因此，|MN|=

4x02+(5- 20 9 x02)-8x0 (x0-2)2

=

16 9 x02-8x0+5 (x0-2)2

，

记F（x₀）=

16 9 x02-8x0+5

(x0-2)2

，得F'（x）=

8 9 x0+6

(x0-2)3

∵椭圆上动点P位于y轴左侧，可得x₀∈[-

3

2

，0），而-

3

2

≤x₀＜0时F'（x）=

8 9 x0+6

(x0-2)3

＜0

∴F（x₀）是上的减函数，可得F（x₀）的最大值为F（-

3

2

）=

12

7

，此时|MN|=

2 21

7

因此线段MN的长的最大值为

2 21

7

，出此时点P的坐标为（-

3

2

，0）．