问题
选择题
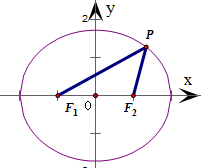
已知点P为椭圆C:
|
答案
∵点P为椭圆C:
+x2 4
=1上动点,y2 3
∴a=2,b=
,可得c=3
=1a2-b2
运动点P可得|PF1|∈[a-c,a+c],即|PF1|∈[1,3]
当P与椭圆的左顶点重合时,|PF1|的最小值为1;当P与椭圆的右顶点重合时,
|PF1|的最大值为3
同理,P与椭圆的左顶点重合时,|PF2|的最大值为3;当P与椭圆的右顶点重合时,|PF2|的最小值为1
∴当P与椭圆的右顶点重合时,|PF1|-|PF2|达到最大值,最大值为3-1=2.
故选:A