问题
计算题
宇航员站在一星球表面上的某高处，沿水平方向抛出一个小球，经过时间t ，小球落到星球表面，测得抛出点与落地点之间的距离为L。若抛出时的初速度增大为原来的2倍，则抛出点与落地点之间的距离为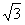
L。已知两落地点在同一水平面上，该星球的半径为R，万有引力常量为G
，求该星球的质量M。
答案
解：设抛出点的高度为H，第一次平抛的水平射程为x，则有
x2+H2=L2①
由平抛运动规律得知，当初速度增大为原来的2倍，其水平射程也增大到2x，可得
(2x)2+H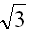2=(
L)2②
由方程①②解得
H=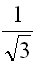
L
设该星球上的“重力加速度”为g，由平抛运动的规律得
H=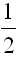
gt2③
由万有引力定律与牛顿第二定律得
mg=G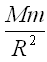
④
式中m为小球的质量，联立以上各式，得
M=