问题
填空题
若直线y=x+b与曲线x=
|
答案
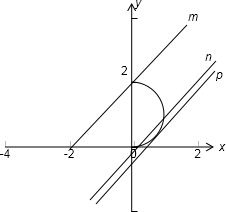
如图所示:
曲线x=
即 x2+(y-1)2=1,x≥0,表示圆心在(0,1),半径等于1,且位于y轴的右侧1-(y-1)2
或y轴上的一个半圆,直线y=x+b的斜率等于1、在y轴上的截距等于b 的一组平行线,
直线m与直线n的斜率都等于1,在y轴上的截距分别为2、0,直线p与半圆相切,斜率也是1,
设直线p方程 x-y+h=0(h<0),由切线的性质得 1=
,∴h=1-|0-1+h| 2 2
满足条件的直线应位于直线m与直线n之间(包括m,不包括n)或是直线p,
∴0<b≤2 或b=1-
,2
故答案为:0<b≤2 或b=1-
.2