问题
解答题
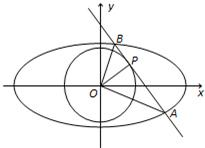
已知椭圆
(Ⅰ)求椭圆的方程; (Ⅱ)已知直线l:y=kx+m为圆x2+y2=
|
答案
(Ⅰ)依题可得:
⇒a=2,b=1,c=e=
=c a 3 2
+1 a2
=13 4b2 a2=b2+c2 3
所以椭圆的方程为:
+y2=1(4分)x2 4
(Ⅱ)由
得(1+4k2)x2+8kmx+4m2-4=0,y=kx+m
+y2=1x2 4
设A(x1,y1)B(x2,y2),
x1+x2=
,x1•x2=-8km 1+4k2
,4m2-4 1+4k2
又
•OA
=x1•x2+y1y2OB
=x1x2+(kx1+m)(kx2+m)
=(k2+1)
+km4m2-4 1+4k2
+m2-8km 1+4k2
=
,5m2-4k2-4 1+4k2
∵直线l与圆x2+y2=
相切,4 5
∴原点O到直线l的距离为:
=|m| 1+k2
∴5m2=4k2+42 5 5
∴x1•x2+y1•y2=0
∴∠AOB为直角.

 ,则可判断该灯标()。
,则可判断该灯标()。