问题
选择题
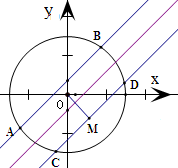
若圆x2+y2=r2(r>0)上仅有4个点到直线x-y-2=0的距离为1,则实数r的取值范围是( )
|
答案
作出到直线x-y-2=0的距离为1的点的轨迹,得到与直线x-y-2=0平行,
且到直线x-y-2=0的距离等于1的两条直线,
∵圆x2+y2=r2的圆心为原点,
原点到直线x-y-2=0的距离为d=
=|0-0-2| 2
,2
∴两条平行线中与圆心O距离较远的一条到原点的距离为d'=
+1,2
又∵圆x2+y2=r2(r>0)上有4个点到直线x-y-2=0的距离为1,
∴两条平行线与圆x2+y2=r2有4个公共点,即它们都与圆x2+y2=r2相交.
由此可得圆的半径r>d',
即r>
+1,实数r的取值范围是(2
+1,+∞).2
故选:C