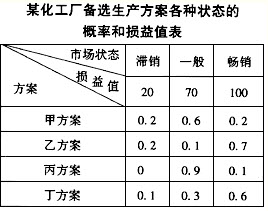
已知抛物线 x2=4y的焦点是椭圆 C:
(I)求椭圆C和圆O的方程; (Ⅱ)已知过点P(0,
(Ⅲ)已知M(x0,y0)是圆O上任意一点,过M点作直线l1,l2,使得l1,l2与椭圆C都只有一个公共点,求证:l1⊥l2. |
(I)由x2=4y可得抛物线焦点坐标为(0,1),∴b=1,
又∵e=
,∴3 2
=c2 a2
,∵a2=b2+c2,∴a2=4,3 4
∴
=a2+b2
,5
∴椭圆C的方程为
+y2=1,圆O的方程为x2+y2=5.x2 4
(Ⅱ)∵过点P(0,
)的直线l与椭圆C在第一象限内只有一个公共点,5
∴直线l的斜率存在,设l的方程为y=kx+
,k<05
由
,得x2+4(kx+y=kx+ 5
+y2=1x2 4
)2=4,5
即(1+4k2)x2+8
kx+16=0,5
则△=(8
k)2-64(1+4k2)=0,5
∴k2=1,又k<0,k=-1,
∴直线l方程为y=-x+
,5
圆心O到直线l方程为y=-x+
,5
圆心O到直线l的距离d=
=5 2
,10 2
∴直线l被圆O截得的弦长为2
=5-(
)210 2
.10
(Ⅲ)证明:若点M的坐标为(2,1),(2,-1),(-2,-1),(-2,1),
则过这四点分别作满足条件的直线l1,l2,
若一条直线斜率为0,则另一条斜率不存在,则l1⊥l2
若直线l1,l2斜率都存在,则设过M与椭圆只有一个公共点的直线方程为y-y0=k(x-x0),
由
,得x2+4[kx+(y0-kx0)]2=4,y=kx+(y0-kx0)
+y2=1x2 4
即(1+4k2)x2+8k(y0-kx0)•x+4(y0-kx0)2-4=0,
则△=[8k(y0-kx0)]2-4(1+4k2)[4(y0-kx0)2-4]=0,
化简得(4-x02)k2+2x0y0k+1-y02=0,
∵x02+y02=5,
∴(4-x02)k2+2x0yk+x02-4=0,
设l1,l2的斜率分别为k1,k2,因为l1,l2与椭圆都只有一个公共点,
所以k1,k2满足(4-x02)k2+2x0yk+x02-4=0,
∴k1•k2=
=-1,x02-4 4-x02
∴l1⊥l2.