证明:如图,以顶点A为坐标原点,以AB所在直线为x轴建立直角坐标系,则A(0,0).

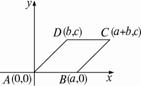
设B(a,0),D(b,c),由平行四边形的性质得点C的坐标为(a+b,c),

因为|AB|²=a²,|CD|²=a²,|AD|²=b²+c²,|BC|²=b²+c²,|AC|²=(a+b)²+c²,|BD|²=(b-a)²+c²,

所以|AB|²+|CD|²+|AD|²+|BC|²=2(a²+b²+c²),

|AC|²+|BD|²=2(a²+b²+c²).

所以|AB|²+|CD|²+|AD|²+|BC|²=|AC|²+|BD|².

因此,平行四边形四条边的平方和等于两条对角线的平方和.

两条相交直线的夹角、点到直线的距离公式