问题
填空题
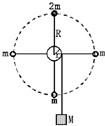
如图所示,固定转轴的半径为r,通过绕在轴上的细线悬挂一质量为M的重物,轴与细线的质量均不计,轴四周有四根轻杆,杆端安装四个小球,最高位置的小球质量为2m,其余三个小球的质量均为m,球离轴心的距离均为R.现从静止开始释放,整个装置发生运动,则当最高位置的小球第一次转至最低位置时,物体M的速度大小为______.
答案
系统释放的势能等于系统的动能的增加,释放的势能为:△EP=mgR+Mgπr
设此时M的速度为v,则转轴的角速度为
,四个小球的线速度为v r vR r
因此系统的动能△EK=0.5Mv2+3×0.5m(
)2+0.5×2m(vR r
)2vR r
解得:v=r2g(2mR+Mπr) 5mR2+Mr2
故答案为:r2g(2mR+Mπr) 5mR2+Mr2
