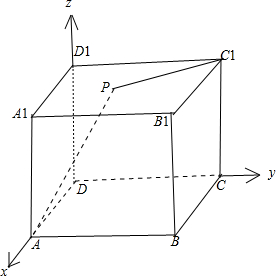
如图所示：以点D为原点，以DA所在的直线为x轴，以DC所在的直线为y轴，以DD₁所在的直线为z轴，

建立空间直角坐标系．

则点A（1，0，0），C₁（0，1，1），设点P的坐标为（x，y，z），则由题意可得 0≤x≤1，0≤y≤1，z=1．

∴

PA

=（1-x，-y，-1），

PC1

=（-x，1-y，0），

∴

PA

•

PC1

=-x（1-x）-y（1-y）+0=x²-x+y²-y=(x-

1

2

)2+(y-

1

2

)2-

1

2

，

由二次函数的性质可得，当x=y=

1

2

时，

PA

•

PC1

取得最小值为-

1

2

；

故当x=0或1，且y=0或1时，

PA

•

PC1

取得最大值为0，

则

PA

•

PC1

的取值范围是[-

1

2

，0]，

故选D．