问题
选择题
已知
|
答案
由题意可得-
=b
+a
,平方可得 3c
2=a
2+2a
•a
+c
2=c
2+2|a
|•|a
|•cos60°+c
2.c
即2|
|2=|a
|•|a
|+|c
|2,|c
|2-|a
|2=|c
|•|a
|-|c
|2,a
∴(|
|+|a
|)(|c
|-|a
|)=|c
|(|a
|-|c
|),a
化简可得 (|
|-|a
|)•(2|c
|+|a
|)=0,∴|c
|=|c
|.a
故以
、a
为邻边的平行四边形是一个菱形.c
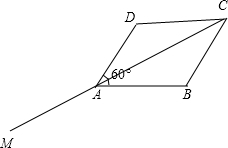
如图所示:设
=AB
,a
=AD
,则c
=AC
+a
,s设c
=-AM
,AC
由
与a
的夹角等于60°,可得∠BAD=60°,∠BAC=30°,故∠MAB=150°,即c
、a
的夹角等于150°,b
∴cos<
,a
>=cos150°=-b
,3 2
故选D.