问题
问答题
如图6-7-9所示,质量为m的小物体在水平转台上随转台以频率f作匀速圆周运动,物体到转轴的距离为d、物体与转台摩擦因素为μ,求:
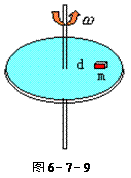
(1)物体所需要的向心力?
(2)
1)物体所受到的转台对它的支持力?摩擦力?
(3)
为使物体保持距离d随转台一起转动,转台转动的角速度应满足什么条件?
答案
(1)m(2πf)2d,(2)G,m(2πf)2d,(3)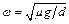 。
。
(1)物体随转台做圆周运动其向心加速度a=ω2r=(2πf)2d,由牛顿第二定律得F向=m(2πf)2d.
(2)物体在竖直直方向上处理平衡状态,所以物体受到平台的支持力为G,物体在水平面内只可能受到摩擦力,所以摩擦力提供物体做圆周运动的向心力,Fμ= F向=m(2πf)2d.
(3)物体受到的滑动摩擦力近似等于最大静摩擦力,当物体所受到的摩擦力不足以改变物体的速度的方向时,物体将相对平台发生滑动,所以μmg=mω2d,即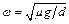 。
。