问题
选择题
如图9所示，轻杆长为3L，在杆的A、B两端分别固定质量均为m的球A和球B，杆上距球A为L处的点O装在光滑的水平转动轴上，外界给予系统一定的能量后，杆和球在竖直面内转动．在转动的过程中，忽略空气的阻力．若球B运动到最高点时，球B对杆恰好无作用力，则下列说法正确的是（ ）
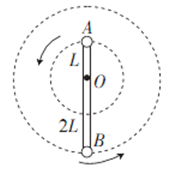
A．球B在最高点时速度为零
B．此时球A的速度也为零
C．球B在最高点时，杆对水平轴的作用力为1.5mg
D．球B转到最低点时，其速度为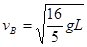
答案
答案：C
A、由牛顿第二定律得：mg=m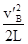
，得到球B在最高点时速度vB′=
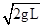．故A错误．
B、由v=ωr，ω相同，得到此时球A的速度为vA′=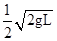
．故B错误．
C、球B在最高点时，A在最低点，以A为研究对象，由牛顿第二定律得
F-mg=m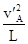
代入解得F=1.5mg
则杆对水平轴的作用力为1.5mg．故C正确．
D、球B从最高转到最低点过程中，以O点参考，根据系统机械能守恒得
mg?2L-mgL+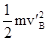
+
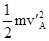=mgL-mg?2L+
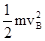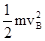+，又vB=2vA
代入解得vB=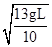
．故D错误．
故选C