问题
解答题
如图,正五边形ABCD中,点F、G分别是BC、CD的中点,AF与BG相交于H。
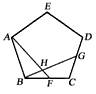
(1)求证:△ABF≌△BCG;
(2)求∠AHG的度数。
答案
解:(1)证明:∵五边形ABCDE是正五边形,
∴AB=BC=CD,∠ABC=∠BCD,
∵F、G分别是BC、CD的中点,
∴BF=CG,
在△ABF和△BCG中,
AB=BC,∠ABC=∠BCD,BF=CG,
∴△ABF≌△BCG;
(2)由(1)知∠GBC=∠FAB,
∵∠AHG=∠FAB+∠ABH=∠GBC+∠ABH=∠ABC,
∵正五边形的内角为108°,
∴∠AHG=108°。
