问题
解答题
已知正n边形的周长为60，边长为a。
⑴当n=3时，请直接写出a的值；
⑵把正n边形的周长与边数同时增加7后，假设得到的仍是正多边形，它的边数为n+7，周长为67，边长为b。有人分别取n等于3、20、120，再求出相应的a与b，然后断言：“无论n取任何大于2的正整数，a与b一定不相等。”你认为这种说法对吗？若不对，请求出不符合这一说法的n的值。
答案
解（1）a=20；
（2）此说法不正确理由如下：
尽管当n=3、20、120时，a>b或a<b，
但可令a=b，得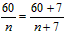
，
即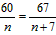
（*），
∴60n+420=67n，解得n=60
经检验n=60是方程（*）的根，
∴当n=60时，a=b，即不符合这一说法的n的值为60。