问题
证明题
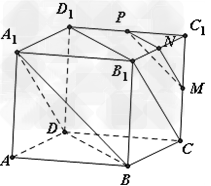
在正方体AC1中，M、N、P分别是棱CC1、B1C1、C1D1的中点．求证：面MNP∥面A1BD．
答案
解：连接B1D1、B1C，
∵正方体AC1中，A1B1∥CD且A1B1=CD
∴四边形A1B1CD是平行四边形，
可得A1D∥CB1
又∵△B1C1C中，M、N分别是CC1、B1C1的中点．
∴MN∥CB1
∴A1D∥MN
∵MN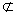
平面A1BD，A1D
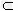平面A1BD，
∴MN∥平面A1BD．
同理，可得PN∥平面A1BD．
∵MN、PN是平面MNP内的相交直线
∴平面MNP∥平面A1BD
