问题
计算题
如图9所示,半径为R,内径很小的光滑半圆管竖直放置。两个质量均为m的小球a、b以不同的速度进入管内,a通过最高点A时,对管壁上部的压力为3mg,b通过最高点A时,对管壁下部的压力为0.75mg,求a、b两球落地点间的距离。
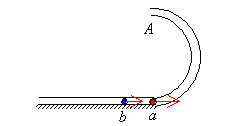
答案
s=3R
在最高点C时对管壁上部的压力为3mg,根据牛顿第三定律,管壁对A向下的压力为3mg,由于在C时处于圆周运动的最高点,所以合外力提供向心力
mg+3mg=mvA2/R ( 2分 )
vA= 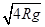
A离开C做平抛运动,下降2R落地 落地时间t
2R=gt2/2 ( 2分 )
Sa=VAt
可得Sa="4R" ( 2分 )
同理B通过最高点C时,对管壁的下端的压力为0.75mg,根据牛顿第三定律,管壁对B向上的支持力0.75mg
mg-0.75mg=mvB2/R
vB= 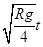
SB= vB t
可得SB="R" ( 2分 )
所以A、B两球落地点间的距离
s=Sa-SB=4R-R=3R ( 2分 )
