证明：∵正方体ABCD-A₁B₁C₁D₁中，M是AA₁的中点，作图如下：

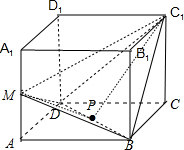
不妨设该正方体的边长为1，取BD的中点为P，连接MP，C₁P，

∵△C₁BD为边长为

2

的等边三角形，点P为BD的中点，

∴C₁P⊥BD，且C₁P=C₁Dsin60°=

2

×

3

2

=

6

2

；

同理，在等腰三角形BMD中，MP⊥BD；①

∴直角三角形MPD中，MD=

12+( 1 2 )2

=

5

2

，PD=

2

2

，

∴MP=

MD2-PD2

=

5 4 - 2 4

=

3

2

；

又C₁M=

C1A12+A1M2

=

2+ 1 4

=

3

2

；

在△C₁MP中，MP=

3

2

，C₁P=

6

2

，C₁M=

3

2

，

∴C1M2=C1P2+MP²，

∴△C₁MP为直角三角形，C₁P⊥MP，②

由①MP⊥BD，②C₁P⊥MP，C₁P∩BD=P，

∴MP⊥平面BDC₁．

又MP⊂平面MBD，

∴平面MBD⊥平面BDC₁．