问题
解答题
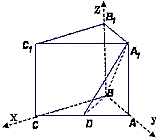
三棱柱中,∠ABC=90°,BB1⊥底面ABC,D为棱AC的中点,且AB=BC=BB1=1。
(1)求二面角A1-BD-C的余弦值;
(2)棱CC1上是否存在一点P,使PD⊥平面A1BD;若存在,试确定P点位置,若不存在,请说明理由。
答案
解:(1)以B为坐标原点,射线BC为x轴的正半轴,
建立如图所示的直角坐标系B-xyz, A(0,1,0),C(1,0,0),
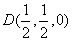 ,
,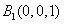 ,
,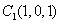 ,
,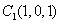 ,
,
设平面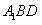 的一个法向量
的一个法向量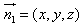 ,
,
又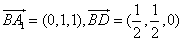 ,
,
∴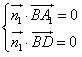 ,
,
令x=1,可得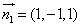 ,
,
又平面BDC的一个法向量为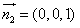 ,
,
设二面角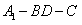 的大小为
的大小为 ,可知
,可知 为钝角,故
为钝角,故 。
。
(2)设P(1,0,z),则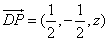 ,
,
要使PD⊥平面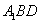 ,则需
,则需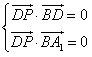 ,
,
可得 ,故
,故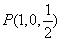 ,
,
即当P是CC1的中点时,所以PD⊥平面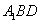 。
。