问题
证明题
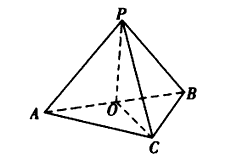
已知P是直角三角形ABC所在平面外一点,O是斜边AB的中点,且PA=PB=PC。
求证:PO⊥平面ABC。
答案
证明:连接OC,如图所示,
∵AB是Rt△ABC的斜边,O是AB的中点,
∴OA=OB=OC,
∵PA=PB=PC,
∴△POA≌△POB≌△POC,
∴∠POA=∠POB=∠POC,
∵∠POA+∠POB=180°,
∴∠POA=∠POB=90°,
∴∠POC=90°,即PO⊥OA ,PO⊥OC,
∵OA∩OC=O,
∴PO⊥平面ABC。
