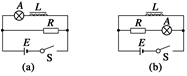
问题
计算题
如图所示，在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球，圆锥顶角为2θ，当圆锥和球一起以角速度ω匀速转动时，球压紧锥面。
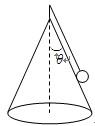
(1)此时绳的张力是多少？
(2)若要小球离开锥面，则小球的角速度至少为多少？
答案
(1)T=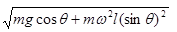
(2)ω＞
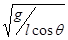
题分析：(1)小球此时受到竖直向下的重力mg，绳子的拉力T，锥面对小球的支持力，三个力作用，合力充当向心力，即合力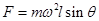
在水平方向上有，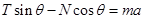
，
，
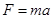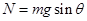
联立四个式子可得T=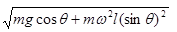
（2）重力和拉力完全充当向心力时，小球对锥面的压力为零，，
故有向心力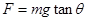
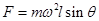，，联立可得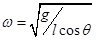
点评：关键是对小球受力分析，判断向心力来源，根据牛顿第二定律列式求解
