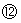如图所示,质量M=2kg的滑块套在光滑的水平轨道上,质量m=1kg的小球通过长L=0.5m的轻质细杆与滑块上的光滑轴O连接,小球和轻杆可在竖直平面内绕O轴自由转动,开始轻杆处于水平状态,现给小球一个竖直向上的初速度v0="4" m/s,g取10m/s2。
(1)若锁定滑块,试求小球通过最高点P时对轻杆的作用力大小和方向。
(2)若解除对滑块的锁定,试求小球通过最高点时的速度大小。
(3)在满足(2)的条件下,试求小球击中滑块右侧轨道位置点与小球起始位置点间的距离。
(1)2N(2)2m/s(3)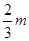
(1)设小球能通过最高点,且此时的速度为 ,在上升过程中,因只有重力做功,小球的机械能守恒。则
,在上升过程中,因只有重力做功,小球的机械能守恒。则
 ①
①
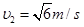 ②
②
设小球到达最高点时,轻杆对小球的作用力为F,方向向下,则 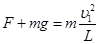 ③
③
由②③式,得 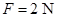 ④
④
由牛顿第三定律可知,小球对轻杆的作用力大小为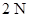 ,方向竖直向上。
,方向竖直向上。
(2)解除锁定后,设小球通过最高点时的速度为 ,此时滑块的速度为V。在上升过程中,因系统在水平方向不受外力作用,水平方向的动量守恒。以水平向右的方向为正方向,有
,此时滑块的速度为V。在上升过程中,因系统在水平方向不受外力作用,水平方向的动量守恒。以水平向右的方向为正方向,有
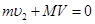 ⑤
⑤
在上升过程中,因只有重力做功,系统的机械能守恒,则
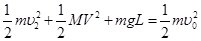 ⑥
⑥
由⑤⑥式,得 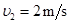 ⑦
⑦
(3)设小球击中滑块右侧轨道的位置点与小球起始位置点间的距离为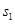 ,滑块向左移动的距离为
,滑块向左移动的距离为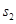 ,任意时刻小球的水平速度大小为
,任意时刻小球的水平速度大小为 ,滑块的速度大小为
,滑块的速度大小为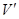 。由系统水平方向的动量守恒,得
。由系统水平方向的动量守恒,得 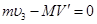 ⑧
⑧
将⑧式两边同乘以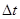 ,得
,得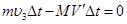 ⑨
⑨
因⑨式对任意时刻附近的微小间隔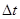 都成立,累积相加后,有
都成立,累积相加后,有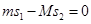 ⑩
⑩
又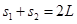
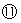
由⑩ 式得
式得