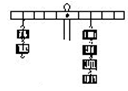
如图所示,在竖直平面内有一水平向右的匀强电场,场强E=1.0×104 N/C.电场内有一半径R=2.0 m的光滑绝缘细圆环形轨道竖直放置且固定,有一质量为m=0.4 kg、带电荷量为q=+3.0×10-4 C的带孔小球穿过细圆环形轨道静止在位置A,现对小球沿切线方向作用一瞬时速度vA,使小球恰好能在光滑绝缘细圆环形轨道上做圆周运动,取圆环的最低点为重力势能和电势能的零势能点.已知g=10 m/s2,sin 37°=0.6,cos 37°=0.8,求:

(1)瞬时速度vA的大小;
(2)小球机械能的最小值.
(1)10 m/s (2)12 J
(1)如图所示,小球的平衡位置在A点,此时重力与电场力的合力F与重力的夹角为θ,则tan θ=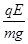 =
=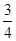 ,θ=37°,
,θ=37°,
F=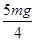 .
.
小球速度最小时的位置在过平衡位置的直径的另一端B,且vB=0,从B位置到A位置,由动能定理有
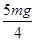 ×2R=
×2R=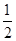 m(v
m(v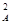 -v
-v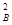 )
)
代入数据得vA=10 m/s.
(2)由功能关系可知,除重力外的其他力做负功越多,小球的机械能越小,因此小球机械能的最小值的位置在小球电势能的最大值的位置,即在图中D位置,设机械能的最小值为Emin,则由能量守恒定律得
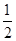 mv
mv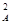 +mgR(1-cos θ)-EqR(1+sin θ)=Emin.代入数据得Emin=12 J.
+mgR(1-cos θ)-EqR(1+sin θ)=Emin.代入数据得Emin=12 J.