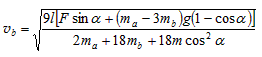问题
计算题
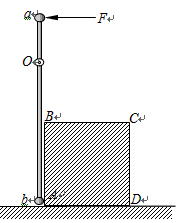
如图所示,一根长为l的细刚性轻杆的两端分别连结小球a和b,它们的质量分别为ma和 mb。杆可绕距a球为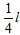 处的水平定轴O在竖直平面内转动。初始时杆处于竖直位置。小球b几乎接触桌面。在杆的右边水平桌面上,紧挨着细杆放着一个质量为m的立方体匀质物块,图中ABCD为过立方体中心且与细杆共面的截面。现用一水平恒力F作用于a球上,使之绕轴逆时针转动,求当a转过
处的水平定轴O在竖直平面内转动。初始时杆处于竖直位置。小球b几乎接触桌面。在杆的右边水平桌面上,紧挨着细杆放着一个质量为m的立方体匀质物块,图中ABCD为过立方体中心且与细杆共面的截面。现用一水平恒力F作用于a球上,使之绕轴逆时针转动,求当a转过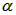 角时小球b速度的大小。设在此过程中立方体物块没有发生转动,且小球b与立方体物块始终接触没有分离。不计一切摩擦。
角时小球b速度的大小。设在此过程中立方体物块没有发生转动,且小球b与立方体物块始终接触没有分离。不计一切摩擦。
答案
解:如图所示,用表示a转过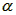 角时b球速度的大小,v表示此时立方体速度的大小,则有
角时b球速度的大小,v表示此时立方体速度的大小,则有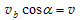 ① 由于b与正立方体的接触是光滑的,相互作用力总是沿水平方向,而且两者在水平方向的位移相同,因此相互作用的作用力和反作用力做功大小相同,符号相反,做功的总和为0。因此在整个过程中推力F所做的功应等于球a、b和正立方体机械能的增量。现用
① 由于b与正立方体的接触是光滑的,相互作用力总是沿水平方向,而且两者在水平方向的位移相同,因此相互作用的作用力和反作用力做功大小相同,符号相反,做功的总和为0。因此在整个过程中推力F所做的功应等于球a、b和正立方体机械能的增量。现用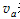 表示此时a球速度的大小,因为a、b角速度相同,
表示此时a球速度的大小,因为a、b角速度相同, ,
,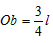 ,所以得
,所以得 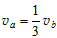 ②
②
根据功能原理可知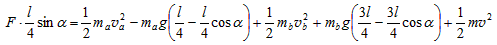 ③
③
将①、②式代入可得
解得