问题
填空题
过△ABC所在平面R外一点P作P0⊥α,垂足为0,连接PA,PB,PC
(1)若PA=PB=PC,则点0是△ABC的______ 心;
(2)若PA⊥PB,PB⊥PC,PC⊥PA,则点0是△ABC的______心.
答案
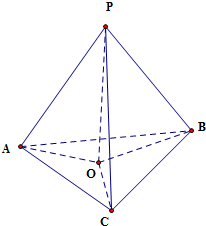
(1)若PA=PB=PC,
∵P0⊥α,垂足为0,
∴Rt△PAO≌Rt△PBO≌Rt△PBO
可得AO=BO=CO,得点0是△ABC的外心
(2)若PA⊥PB,PC⊥PA,PC⊥PA,
∵PB、PC是平面PBC内的相交直线
∴PA⊥平面PBC,可得PA⊥BC
∵AO是PA在平面ABC内的射影,
∴AO⊥BC,同理可得BO⊥AC、CO⊥AB
因此,点0是△ABC的垂心
故答案为:外、垂
