依题意,f/(x)=x-(2a+1)+…(1分)y0=f(x0),曲线y=f(x)在点P(x0,y0)处的切线为y-y0=f/(x0)(x-x0)…(2分),
即y=y0+f/(x0)(x-x0),所以g(x)=y0+f/(x0)(x-x0)…(3分)
直接计算得g(x)=x0x-x02-(2a+1)x+(a2+a)(lnx0+-1)…(5分),
直接计算得f(x)≥g(x)等价于(x-x0)2+(a2+a)(ln0-+1)≥0…(7分)
记h(x)=(x-x0)2+(a2+a)(ln-+1),则h/(x)=(x-x0)+(a2+a)(-)=(x-x0)(1-)…(8分)
若a2+a≤0,则由h′(x)=0,得x=x0…(9分),
且当0<x<x0时,h′(x)<0,当x>x0时,h′(x)>0…(10分),
所以h(x)在x=x0处取得极小值,从而也是最小值,即h(x)≥h(x0)=0,从而f(x)≥g(x)恒成立…(11分).
若a2+a>0,取x0=,则h/(x)=(x-x0)(1-)≥0,
且当x1≠x0时h′(x)>0,h(x)单调递增…(12分),
所以当0<x<x0时,h(x)<h(x0)=0,与f(x)≥g(x)恒成立矛盾,所以a2+a≤0…(13分),
从而a的取值范围为-1≤a≤0…(14分)

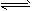 2SO3经一段时间后,SO3的浓度增加了0.4mol/L,在这段时间内用O2表示的反应速率为0.04 mol/(L·s)。则这段时间为 [ ]
2SO3经一段时间后,SO3的浓度增加了0.4mol/L,在这段时间内用O2表示的反应速率为0.04 mol/(L·s)。则这段时间为 [ ]