问题
计算题
一段铁路转弯处，内外轨高度差为h=10 cm，弯道半径为r =625 m，轨距l=1 435 mm，求这段弯道的设计速度v0 是多大？并讨论当火车速度大于或小于v0时内外轨的侧压力 (g= 10m/s2)．
答案
解;
当火车以设计速度v0运行时，其受力示意图如图1所示，其中G与FN的合力F=mgtanθ提供火车转弯的向心力，又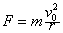
，所以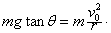
当θ很小时，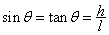
，代入上式有
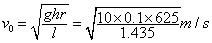= 20. 87 m/s．
讨论：当v>v0时，外轨对外轮边缘产生沿路面向内的弹力（侧压力），此时火车受力如图2所示，设火车的质量为 m，根据牛顿第二定律有
FNsinθ+F外cosθ=
①
FNcosθ= F外sinθ+ mg. ②
联立①②两式解得
F外=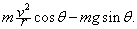
由此看出，火车的速度v越大，F外越大，铁轨容易损坏，若F外过大，会造成铁轨的侧向移动，损坏铁轨，造成火车出轨．
当v< v0时，内轨对内轮缘产生沿路面向外的侧压力以抵消多余的向心力，同理有
FNsinθ - F内cosθ =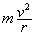
③
FNcosθ+F内sinθ= mg. ④
联立③④两式解得
F内= mgsinθ- 
可以看出，v越小，F内越大，内轨的磨损也较大，因此在有弯道限速标志的地方一定要遵守规定．
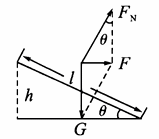
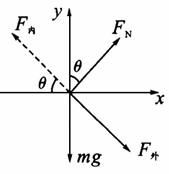
图1 图2