问题
选择题
已知函数y=f(x)是R上的可导函数,当x≠0时,有f′(x)+
|
答案
由F(x)=xf(x)+
=0,得xf(x)=-1 x
,1 x
设 g(x)=xf(x),
则g′(x)=f(x)+xf′(x),
∵x≠0时,有f′(x)+
>0,f(x) x
∴x≠0时,
>0,f(x)+xf′(x) x
即当x>0时,g'(x)=f(x)+xf'(x)>0,此时函数g(x)单调递增,
此时g(x)>g(0)=0,
当x<0时,g'(x)=f(x)+xf'(x)<0,此时函数g(x)单调递减,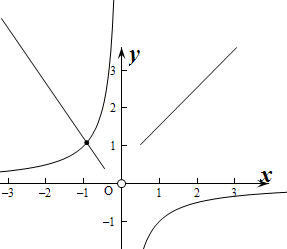
此时g(x)>g(0)=0,
作出函数g(x)和函数y=-
的图象,(直线只代表单调性和取值范围),由图象可知函数F(x)=xf(x)+1 x
的零点个数为1个.1 x
故选:B.
