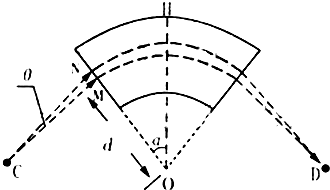
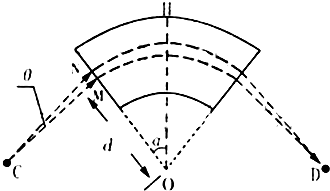
如图为一种质谱仪工作原理示意图.在以O为圆心,OH为对称轴,夹角为2α的扇形区域内分布着方向垂直于纸面的匀强磁场.对称于OH轴的C和D分别是离子发射点和收集点.CM垂直磁场左边界于M,且OM=d.现有一正离子束以小发散角(纸面内)从C射出,这些离子在CM方向上的分速度均为v0.若该离子束中比荷为
的离子都能汇聚到D,试求:q m
(1)磁感应强度的大小和方向(提示:可考虑沿CM方向运动的离子为研究对象);
(2)离子沿与CM成θ角的直线CN进入磁场,其轨道半径和在磁场中的运动时间;
(3)线段CM的长度.
(1)
设沿CM方向运动的离子在磁场中做圆周运动的轨道半径为R
由 qv0B=m v 20 R
又 R=d
得 B=mv0 qd
磁场方向垂直纸面向外
(2)
设沿CN运动的离子速度大小为v,在磁场中的轨道半径为R′,运动时间为t
由vcosθ=v0
得v=v0 cosθ
R′=mv qB
=d cosθ
离子在磁场中做匀速圆周运动的周期T=2πm qB
t=T×θ+α π
=
d2(θ+α) v0
(3)
设圆心为A,过A做AB垂直NO,
可以证明NM=BO
∵NM=CMtanθ
又∵BO=ABcotα
=R′sinθcotα
=
sinθcotαd cosθ
∴CM=dcotα
