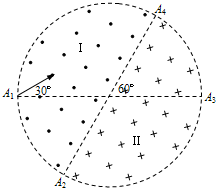
如图所示,在一个圆形区域内,两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中,A2A4与A1A3的夹角为60°.一质量为m、带电量为+q的粒子以某一速度从Ⅰ区的边缘点A1处沿与A1A3成30°角的方向射入磁场,随后该粒子以垂直于A2A4的方向经过圆心O进入Ⅱ区,最后再从A4处射出磁场.已知该粒子从射入到射出磁场所用的时间为t,求Ⅰ区和Ⅱ区中磁感应强度的大小(忽略粒子重力).
设粒子的入射速度为v,已知粒子带正电,故它在磁场中先顺时针做圆周运动,再逆时针做圆周运动,最后从A4点射出,用B1、B2、R1、R2、T1、T2分别表示在磁场Ⅰ区Ⅱ磁感应强度、轨道半径和周期qvB1=m
①v2 R1
qvB2=m
②v2 R2
T1=
=2πR1 v
③2πm qB1
T2=
=2πR2 v
④2πm qB2
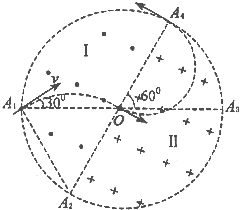
设圆形区域的半径为r,如答图5所示,已知带电粒子过圆心且垂直A3A4进入Ⅱ区磁场,连接A1A2,△A1OA2为等边三角形,A2为带电粒子在Ⅱ区磁场中运动轨迹的圆心,其半径R1=A1A2=OA2=r⑤
圆心角∠A1A2O=60°,带电粒子在Ⅰ区磁场中运动的时间为t1=
T1⑥1 6
带电粒子在Ⅱ区磁场中运动轨迹的圆心在OA4的中点,即R=
r ⑦1 2
在Ⅱ区磁场中运动时间为t2=
T2⑧1 2
带电粒子从射入到射出磁场所用的总时间t=t1+t2⑨
由以上各式可得B1=5 6
⑩B2=πM qt 5 3 πM qt
故I区磁感应强度为5 6
;II区磁感应强度为πM qt 5 3
.πM qt
