问题
解答题
在等腰△ABC中,三边分别为a、b、c,其中a=5,若关于x的方程x2+(b+2)x+6﹣b=0有两个相等的实数根,求△ABC的周长.
答案
解:∵关于x的方程x2+(b+2)x+6﹣b=0有两个相等的实数根,
∴△=(b+2)2﹣4(6﹣b)=0,
即b2+8b﹣20=0;解得b=2,b=﹣10(舍去);
①当a为底,b为腰时,则2+2<5,构不成三角形,此种情况不成立;
②当b为底,a为腰时,则5﹣2<5<5+2,能够构成三角形;此时△ABC的周长为:5+5+2=12;
答:△ABC的周长是12.

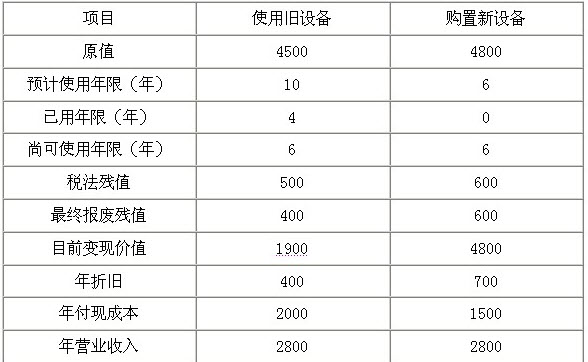 资料二:相关货币时间价值系数如表7所示。 表7 货币时间价值系数
资料二:相关货币时间价值系数如表7所示。 表7 货币时间价值系数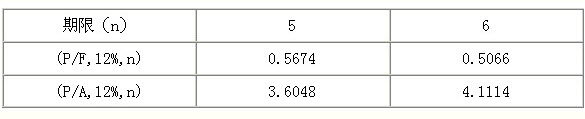 要求:
要求: