问题
填空题
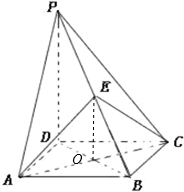
四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,且PD=
|
答案
连接AC,BD,交于O,连接OE,则
∵PD⊥底面ABCD,AC⊂底面ABCD,
∴PD⊥AC,
∵四棱锥P-ABCD的底面是正方形,
∴AC⊥BD
∵PD∩BD=D
∴AC⊥平面PDB
∴∠AEO为AE与平面PDB所成的角,
设AB=a,则PD=
a,∴OE=2
a2 2
∵AO=
a,∴AE=a,2 2
∴sin∠AEO=
=AO AE 2 2
∴∠AEO=45°