问题
解答题
求证：等腰三角形两腰上的高相等．
答案
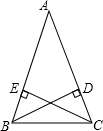
已知：AB=AC，CE⊥AB于E，BD⊥AC于D．
求证：BD=CE．
证明：∵AB=AC，CE⊥AB于E，BD⊥AC于D，
∴∠AEC=∠ADB=90°，
∵AB=AC，∠A=∠A，
∵△ACE≌△ABD，
∴CE=BD．
搜题请搜索小程序“爱下问搜题”
求证：等腰三角形两腰上的高相等．
已知：AB=AC，CE⊥AB于E，BD⊥AC于D．
求证：BD=CE．
证明：∵AB=AC，CE⊥AB于E，BD⊥AC于D，
∴∠AEC=∠ADB=90°，
∵AB=AC，∠A=∠A，
∵△ACE≌△ABD，
∴CE=BD．