问题
选择题
在等腰三角形ABC中，底边上的高是
|
答案
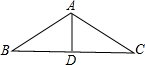
∵AD⊥BC，
∴∠ADB=90°，
∵∠BAD=60°，
∴∠B=30°，
∴AB=2AD=2
，3
在Rt△BDA中，由勾股定理得：BD=3，
同理可求CD=3，
∴BC=6，
∴△ABC的面积是
×BC×AD=1 2
×6×1 2
=33
，3
故选D．
搜题请搜索小程序“爱下问搜题”
在等腰三角形ABC中，底边上的高是
|
∵AD⊥BC，
∴∠ADB=90°，
∵∠BAD=60°，
∴∠B=30°，
∴AB=2AD=2
，3
在Rt△BDA中，由勾股定理得：BD=3，
同理可求CD=3，
∴BC=6，
∴△ABC的面积是
×BC×AD=1 2
×6×1 2
=33
，3
故选D．