问题
解答题
已知矩形ABCD,AB=2BC=2a,AB、CD的中点M、N,以MN为折线翻折平面AMND,使平面AMND⊥平面MBCN,P为MD上一点,Q为BN上一点,且有MP=BQ.
(1)求证PQ∥平面DNC;
(2)求证PQ⊥MN.
答案
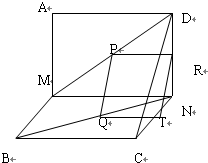
证明:(1)作PR∥MN交DN于R,作QT∥MN交于T,连接RT.
∵∠MDN=∠BNC=45°,DM=NB,PM=QB,PR∥MN,QT∥MN,
∴PR∥QT,且Rt△DRP≌Rt△NTQ,得PR=QT.
∴四边形PQTR为平行四边形,
∴PQ∥RT,
∴PQ∥平面DNC.
(2)证明:如图,
∵RN⊥平面MBCN,NT⊥MN,
∴RT⊥MN,
又∵PQ∥RT,
∴PQ⊥MN.
